Question

The set of all real values $\mathrm{\lambda }$ for which the function $f\left(x\right)=\left(1-{\cos }^{2}x\right). \left(\mathrm{\lambda }+\sin x\right), \mathrm{x\epsilon } \left(-\frac{\mathrm{\pi }}{2}, \frac{\mathrm{\pi }}{2}\right)$, has exactly one maxima and exactly one minima, is :

JEE Main 2020 (06 Sep Shift 2)

Options

• A: $\left(-\frac{1}{2}, \frac{1}{2}\right)-\left\{0\right\}$
• B: $\left(-\frac{3}{2}, \frac{3}{2}\right)$
• C: $\left(-\frac{1}{2}, \frac{1}{2}\right)$
• D: $\left(-\frac{3}{2}, \frac{3}{2}\right)-\left\{0\right\}$

Question

Let $f\left(x\right)=x{\cos }^{-1}\left(-\sin \left|x\right|\right),x\in \left[-\frac{\pi }{2},\frac{\pi }{2}\right],$ then which of the following is true?

JEE Main 2020 (08 Jan Shift 1)

Options

• A: $f\text{'}$ is increasing in $\left(-\frac{\pi }{2},0\right)$ and decreasing in $\left(0,\frac{\pi }{2}\right)$
• B: $f^{\text{'}}\left(0\right)=-\frac{\pi }{2}$
• C: $f$ is not differentiable at $x=0$
• D: $f\text{'}$ is decreasing in $\left(-\frac{\pi }{2},0\right)$ and increasing in $\left(0,\frac{\pi }{2}\right)$

Question

A box open from top is made from a rectangular sheet of dimension $a\times b$ by cutting squares each of side $x$ from each of the four corners and folding up the flaps. If the volume of the box is maximum, then $x$ is equal to:

JEE Main 2021 (27 Aug Shift 2)

Options

• A: $\frac{a+b+\sqrt{a^2+b^2-ab}}{6}$
• B: $\frac{a+b-\sqrt{a^2+b^2-ab}}{12}$
• C: $\frac{a+b-\sqrt{a^2+b^2-ab}}{6}$
• D: $\frac{a+b-\sqrt{a^2+b^2+ab}}{6}$

Question

The number of real roots of the equation $e^{4x}+2e^{3x}-e^x-6=0$ is :

JEE Main 2021 (31 Aug Shift 1)

Options

• A: $0$
• B: $1$
• C: $4$
• D: $2$

Question

The minimum value of $\alpha$ for which the equation $\frac{4}{\sin x}+\frac{1}{1-\sin x}=\alpha$ has at least one solution in $\left(0,\frac{\pi }{2}\right)$ is______.

JEE Main 2021 (24 Feb Shift 1)

Enter your answer

Question

For the function $f\left(x\right)=4{\log }_e\left(x-1\right)-2x^2+4x+5,x>1$, which one of the following is NOT correct?

JEE Main 2022 (24 Jun Shift 1)

Options

• A: $f\left(x\right)$ is increasing in $\left(1,2\right)$  and decreasing in $\left(2,\infty \right)$
• B: $f\left(x\right)=-1$ has exactly two solutions
• C: $f^{\text{'}}\left(\mathrm{e}\right)-f^{"}\left(2\right)<0$
• D: $f\left(x\right)=0$ has a root in the interval $\left(e,e+1\right)$

Question

The sum of absolute maximum and absolute minimum values of the function $f\left(x\right)=\left|2x^2+3x-2\right|+\sin x\cos x$ in the interval $\left[0,1\right]$ is

JEE Main 2022 (24 Jun Shift 1)

Options

• A: $3+\frac{\sin \left(1\right){\cos }^2\left({\displaystyle \frac{1}{2}}\right)}{2}$
• B: $3+\frac{1}{2}\left(1+2\cos \left(1\right)\right)\sin \left(1\right)$
• C: $5+\frac{1}{2}\left(\sin \left(1\right)+\sin \left(2\right)\right)$
• D: $2+\sin \left(\frac{1}{2}\right)\cos \left(\frac{1}{2}\right)$

Question

The number of distinct real roots of the equation $x^7-7x-2=0$ is

JEE Main 2022 (24 Jun Shift 2)

Options

• A: $5$
• B: $7$
• C: $1$
• D: $3$

Question

If the absolute maximum value of the function $f\left(x\right)=\left({\mathrm{x}}^2-2\mathrm{x}+7\right){\mathrm{e}}^{\left(4{\mathrm{x}}^3-12{\mathrm{x}}^2-180\mathrm{x}+31\right)}$in the interval $\left[-3,0\right]$ is $f\left(\alpha \right)$, then

JEE Main 2022 (25 Jul Shift 1)

Options

• A: $\alpha =0$
• B: $\alpha =-3$
• C: $\alpha \in \left(-1,0\right)$
• D: $\alpha \in \left(-3,-1\right)$

Question

Let $f:\mathit{R}\to \mathit{R}$ and $g:\mathit{R}\to \mathit{R}$ be two functions defined by $f\left(x\right)={\log }_{\mathrm{e}}\left(x^2+1\right)-{\mathrm{e}}^{-x}+1$ and $g\left(x\right)=\frac{1-2{\mathrm{e}}^{2x}}{{\mathrm{e}}^x}·$ Then, for which of the following range of $\alpha$, the inequality $f\left(g\left(\frac{{\left(\alpha -1\right)}^2}{3}\right)\right)>f\left(g\left(\alpha -\frac{5}{3}\right)\right)$ holds?

JEE Main 2022 (25 Jun Shift 1)

Options

• A: $\left(-2,-1\right)$
• B: $\left(2,3\right)$
• C: $\left(1,2\right)$
• D: $\left(-1,1\right)$

Question

Let $P$ and $Q$ be any points on the curves ${\left(x-1\right)}^2+{\left(y+1\right)}^2=1$ and $y=x^2$, respectively. The distance between $P$ and $Q$ is minimum for some value of the abscissa of $P$ in the interval

JEE Main 2022 (26 Jul Shift 2)

Options

• A: $\left(0,\frac{1}{4}\right)$
• B: $\left(\frac{1}{2},\frac{3}{4}\right)$
• C: $\left(\frac{1}{4},\frac{1}{2}\right)$
• D: $\left(\frac{3}{4},1\right)$

Question

Let $f\left(x\right)=2{\cos }^{-1}x+4{\cot }^{-1}x-3x^2-2x+10,x\in \left[-1,1\right]$. If $\left[a,b\right]$ is the range of the function, then $4a-b$ is equal to

JEE Main 2022 (26 Jun Shift 1)

Options

• A: $11$
• B: $11-\pi$
• C: $11+\pi$
• D: $15-\pi$

Question

A wire of length $22\mathrm{m}$ is to be cut into two pieces. One of the pieces is to be made into a square and the other into an equilateral triangle. Then, the length of the side of the equilateral triangle, so that the combined area of the square and the equilateral triangle is minimum, is

JEE Main 2022 (29 Jun Shift 1)

Options

• A: $\frac{22}{9+4\sqrt{3}}$
• B: $\frac{66}{9+4\sqrt{3}}$
• C: $\frac{22}{4+9\sqrt{3}}$
• D: $\frac{66}{4+9\sqrt{3}}$

Question

Let $f\left(x\right)=\left|\left(x-1\right)\left(x^2-2x-3\right)\right|+x-3,x\in \mathrm{ℝ}$. If $m$ and $M$ are respectively the number of points of local minimum and local maximum of $f$ in the interval $\left(0,4\right)$, then $m+M$ is equal to _____.

JEE Main 2022 (25 Jun Shift 2)

Enter your answer

Question

The number of distinct real roots of the equation $x^5\left(x^3-x^2-x+1\right)+x\left(3x^3-4x^2-2x+4\right)-1=0$ is

JEE Main 2022 (26 Jul Shift 1)

Enter your answer

Question

Let the function $f\left(x\right)=2x^2-{\log }_{e}x,x>0$, be decreasing in $\left(0,a\right)$ and increasing in $\left(a,4\right)$. A tangent to the parabola $y^2=4ax$ at a point $P$ on it passes through the point $\left(8a, 8a-1\right)$ but does not pass through the point $\left(-\frac{1}{a},0\right)$. If the equation of the normal at $P$ is $\frac{x}{\alpha }+\frac{y}{\beta }=1$, then $\alpha +\beta$ is equal to

JEE Main 2022 (26 Jul Shift 1)

Enter your answer

Question

If the sum of all the roots of the equation $e^{2x}-11e^x-45e^{-x}+\frac{81}{2}=0$ is ${\log }_{e}P$, then $P$ is equal to _____.

JEE Main 2022 (27 Jun Shift 1)

Enter your answer

Question

The sum of the abosolute maximum and minimum values of the function $f\left(x\right)=\left|x^2-5x+6\right|-3x+2$ in the interval $\left[-1,3\right]$ is equal to :

JEE Main 2023 (01 Feb Shift 2)

Options

• A: $10$
• B: $12$
• C: $13$
• D: $24$

Question

The absolute minimum value, of the function $f\left(x\right)=\left|x^2-x+1\right|+\left[x^2-x+1\right]$, where $\left[t\right]$ denotes the greatest integer function, in the interval $\left[-1,2\right]$, is

JEE Main 2023 (31 Jan Shift 2)

Options

• A: $\frac{3}{2}$
• B: $\frac{1}{4}$
• C: $\frac{5}{4}$
• D: $\frac{3}{4}$

Question

Let $f:\left[2,4\right]\to \mathrm{ℝ}$ be a differentiable function such that $\left(x{\log }_{e}x\right)f^{\text{'}}\left(x\right)+\left({\log }_{e}x\right)f\left(x\right)+f\left(x\right)\ge 1,x\in \left[2,4\right]$ with $f\left(2\right)=\frac{1}{2}$ and $f\left(4\right)=\frac{1}{2}$.
Consider the following two statements:

(A) $f\left(x\right)\le 1, \text{for all} x\in \left[2,4\right]$

(B) $f\left(x\right)\ge 1/8, \text{for all} x\in \left[2,4\right]$

Then,

JEE Main 2023 (11 Apr Shift 1)

Options

• A: Neither statement $\left(A\right)$ nor statement $\left(B\right)$ is true
• B: Only statement $\left(B\right)$ is true
• C: Both the statements $\left(A\right)$and $\left(B\right)$are true
• D: Only statement $\left(A\right)$ is true

Question

The set of all $a\in \mathrm{ℝ}$ for which the equation $x|x-1|+|x+2|+a=0$ has exactly one real root, is

JEE Main 2023 (13 Apr Shift 1)

Options

• A: $\left(-7,\infty \right)$
• B: $\left(-\infty ,\infty \right)$
• C: $\left(-6,-3\right)$
• D: $\left(-\infty ,-3\right)$

Question

In the figure, ${\mathrm{\theta }}_1+{\mathrm{\theta }}_2=\frac{\mathrm{\pi }}{2}$ and $\sqrt{3}\left(\mathrm{BE}\right)=4\left(\mathrm{AB}\right)$. If the area of $∆\mathrm{CAB}$ is $2\sqrt{3}-3 {\mathrm{unit}}^2$, when $\frac{{\mathrm{\theta }}_2}{{\mathrm{\theta }}_1}$ is the largest, then the perimeter (in unit) of $∆\mathrm{CED}$ is equal to

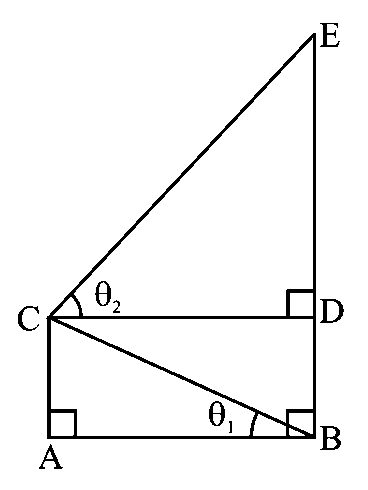
JEE Main 2023 (10 Apr Shift 2)

Enter your answer

Question

Let a rectangle $A B C D$ of sides 2 and 4 be inscribed in another rectangle $P Q R S$ such that the vertices of the rectangle $A B C D$ lie on the sides of the rectangle $P Q R S$. Let $a$ and $b$ be the sides of the rectangle $P Q R S$ when its area is maximum. Then $(a+b)^2$ is equal to :

JEE Main 2024 (05 Apr Shift 1)

Options

• A: 72
• B: 60
• C: 64
• D: 80

Question

For the function $f(x)=\sin x+3 x-\frac{2}{\pi}\left(x^2+x\right), \text { where } x \in\left[0, \frac{\pi}{2}\right],$ consider the following two statements : (I) $\mathrm{f}$ is increasing in $\left(0, \frac{\pi}{2}\right)$. (II) $f^{\prime}$ is decreasing in $\left(0, \frac{\pi}{2}\right)$.
Between the above two statements,

JEE Main 2024 (05 Apr Shift 1)

Options

• A: only (II) is true.
• B: only (I) is true.
• C: neither (I) nor (II) is true.
• D: both (I) and (II) are true

Question

Let the maximum and minimum values of $\left(\sqrt{8 x-x^2-12}-4\right)^2+(x-7)^2, x \in \mathbf{R}$ be $\mathrm{M}$ and $\mathrm{m}$, respectively. Then $\mathrm{M}^2-\mathrm{m}^2$ is equal to _________

JEE Main 2024 (05 Apr Shift 2)

Enter your answer