Question

If $\left|x\right|<1, \left|y\right|<1$ and $x\ne 1$, then the sum to infinity of the following series $\left(x+y\right)+\left(x^2+xy+y^2\right)+\left(x^3+x^{2}y+x{y}^2+y^3\right)+.....$ is

JEE Main 2020 (02 Sep Shift 1)

Options

• A: $\frac{x+y-xy}{\left(1+x\right)\left(1+y\right)}$
• B: $\frac{x+y+xy}{\left(1+x\right)\left(1+y\right)}$
• C: $\frac{x+y-xy}{\left(1-x\right)\left(1-y\right)}$
• D: $\frac{x+y+xy}{\left(1-x\right)\left(1-y\right)}$

Question

Let $a, b, c, d \text{and} p$ be non-zero distinct real numbers such that $\left(a^2+b^2+c^2\right)p^2-2(ab+bc+cd)p+\left(b^2+c^2+d^2\right)=0$. Then

JEE Main 2020 (06 Sep Shift 1)

Options

• A: $a,b,c \text{are in A.P.}$
• B: $a,c,p \text{are in G.P.}$
• C: $a,b,c,d \text{are in G.P.}$
• D: $a,b,c,d \text{are in A.P.}$

Question

Let $a_1,a_2,a_3,\dots$, be a $\mathrm{G}.\mathrm{P}.$ such that $a_1<0,a_1+a_2=4$ and $a_3+a_4=16$. If $\sum _{i=1}^9{a}_i=4\lambda$, then $\lambda$, is equal to.

JEE Main 2020 (07 Jan Shift 2)

Options

• A: $-513$
• B: $-171$
• C: $171$
• D: $\frac{511}{3}$

Question

The sum of the infinite series $1+\frac{2}{3}+\frac{7}{3^2}+\frac{12}{3^3}+\frac{17}{3^4}+\frac{22}{3^5}+\dots \dots$ is equal to:

JEE Main 2021 (26 Feb Shift 1)

Options

• A: $\frac{9}{4}$
• B: $\frac{15}{4}$
• C: $\frac{11}{4}$
• D: $\frac{13}{4}$

Question

Let $x,y>0$. If $x^3{y}^2=2^{15}$, then the least value of $3x+2y$ is

JEE Main 2022 (24 Jun Shift 2)

Options

• A: $30$
• B: $32$
• C: $36$
• D: $40$

Question

Consider two G.Ps. $2,2^2,2^3,\dots$ and $4,4^2,4^3,\dots$ of $60$ and $n$ terms respectively. If the geometric mean of all the $60+n$ terms is ${\left(2\right)}^{\frac{225}{8}}$, then $\sum _{k=1}^{n}k\left(n-k\right)$ is equal to:

JEE Main 2022 (26 Jul Shift 1)

Options

• A: $560$
• B: $1540$
• C: $1330$
• D: $2600$

Question

If $A=\sum _{n=1}^{\infty }\frac{1}{{\left(3+{\left(-1\right)}^n\right)}^n}$ and $B=\sum _{n=1}^{\infty }\frac{{\left(-1\right)}^n}{{\left(3+{\left(-1\right)}^n\right)}^n}$, then $\frac{A}{B}$ is equal to

JEE Main 2022 (26 Jun Shift 2)

Options

• A: $\frac{11}{9}$
• B: $1$
• C: $-\frac{11}{9}$
• D: $-\frac{11}{3}$

Question

If the minimum value of $f\left(x\right)=\frac{5x^2}{2}+\frac{\alpha }{x^5},x>0$, is $14$, then the value of $\alpha$ is equal to

JEE Main 2022 (28 Jul Shift 1)

Options

• A: $32$
• B: $64$
• C: $128$
• D: $256$

Question

The sum $\sum _{n=1}^{21}\frac{3}{\left(4n-1\right)\left(4n+3\right)}$ is equal to

JEE Main 2022 (25 Jul Shift 2)

Options

• A: $\frac{7}{87}$
• B: $\frac{7}{29}$
• C: $\frac{14}{87}$
• D: $\frac{21}{29}$

Question

The series of positive multiples of $3$ is divided into sets : $\left\{3\right\},\left\{6,9,12\right\},\left\{15,18,21,24,27\right\},\dots$ Then the sum of the elements in the ${11}^{\mathrm{th} }$ set is equal to _______.

JEE Main 2022 (26 Jul Shift 1)

Enter your answer

Question

Let $a,b,c$ and $d$ be positive real numbers such that $a+b+c+d=11$. If the maximum value of $a^5{b}^3{c}^{2}d$ is $3750\beta$, then the value of $\beta$ is

JEE Main 2023 (11 Apr Shift 2)

Options

• A: $90$
• B: $110$
• C: $55$
• D: $108$

Question

The sum to $10$terms of the series

$\frac{1}{1+1^2+1^4}+\frac{2}{1+2^2+2^4}+\frac{3}{1+3^2+3^4}+\dots$is :-

JEE Main 2023 (01 Feb Shift 1)

Options

• A: $\frac{59}{111}$
• B: $\frac{55}{111}$
• C: $\frac{56}{111}$
• D: $\frac{58}{111}$

Question

Let $a,b,c>1,a^3,b^3$ and $c^3$ be in $\mathrm{A}.\mathrm{P}.$ and ${\log }_{a}b$, ${\log }_{c}a$ and ${\log }_{b}c$ be in $\mathrm{G}.\mathrm{P}.$ If the sum of first $20$ terms of an $\mathrm{A}.\mathrm{P}.$, whose first term is $\frac{a+4b+c}{3}$ and the common difference is $\frac{a-8b+c}{10}$ is $-444$, then $abc$ is equal to

JEE Main 2023 (30 Jan Shift 2)

Options

• A: $343$
• B: $216$
• C: $\frac{343}{8}$
• D: $\frac{125}{8}$

Question

The $8^{\text{th }}$ common term of the series
$S_1=3+7+11+15+19+\dots$

$S_2=1+6+11+16+21+\dots$. is

JEE Main 2023 (30 Jan Shift 2)

Enter your answer

Question

Let $a_1,a_2,a_3,....,a_n$ be $\mathrm{n}$ positive consecutive terms of an arithmetic progression. If $d>0$ is its common difference, then $\underset{n\to \infty }{\lim }\sqrt{\frac{d}{n}}\left(\frac{1}{\sqrt{a_1}+\sqrt{a_2}}+\frac{1}{\sqrt{a_2}+\sqrt{a_3}}+\dots +\frac{1}{\sqrt{a_{n-1}}+\sqrt{a_n}}\right)$ is

JEE Main 2023 (06 Apr Shift 1)

Options

• A: $\frac{1}{\sqrt{d}}$
• B: $\sqrt{d}$
• C: $1$
• D: $2$

Question

If ${\left(20\right)}^{19}+2\left(21\right){\left(20\right)}^{18}+3{\left(21\right)}^2{\left(20\right)}^{17}+...+20{\left(21\right)}^{19}=k{\left(20\right)}^{19}$, then $k$ is equal to _____.

JEE Main 2023 (06 Apr Shift 2)

Enter your answer

Question

Let $<a_n>$ be a sequence such that $a_1+a_2+...+a_n=\frac{n^2+3n}{\left(n+1\right)\left(n+2\right)}$. If $28\sum _{k=1}^{10}\frac{1}{a_k}=p_1 p_2 p_{3 }... p_m$, where $p_1, p_2, ... p_m$ are the first $m$ prime numbers, then $m$ is equal to

JEE Main 2023 (12 Apr Shift 1)

Options

• A: $5$
• B: $8$
• C: $6$
• D: $7$

Question

Let $A_1$ and $A_2$ be two arithmetic means and $G_1, G_2$ and $G_3$ be three geometric means of two distinct positive numbers. Then $G_1^4+G_2^4+G_3^4+G_1^2{G}_3^2$ is equal to

JEE Main 2023 (15 Apr Shift 1)

Options

• A: ${\left(A_1+A_2\right)}^2{G}_1{G}_3$
• B: $2\left(A_1+A_2\right)G_1{G}_3$
• C: $\left(A_1+A_2\right)G_1^2{G}_3^2$
• D: $2\left(A_1+A_2\right)G_1^2{G}_3^2$

Question

Let $A B C$ be an equilateral triangle. A new triangle is formed by joining the middle points of all sides of the triangle $A B C$ and the same process is repeated infinitely many times. If $\mathrm{P}$ is the sum of perimeters and $Q$ is be the sum of areas of all the triangles formed in this process, then :

JEE Main 2024 (06 Apr Shift 2)

Options

• A: $\mathrm{P}^2=6 \sqrt{3} \mathrm{Q}$
• B: $\mathrm{P}^2=36 \sqrt{3} \mathrm{Q}$
• C: $\mathrm{P}=36 \sqrt{3} \mathrm{Q}^2$
• D: $\mathrm{P}^2=72 \sqrt{3} \mathrm{Q}$

Question

A software company sets up $m$ number of computer systems to finish an assignment in 17 days. If 4 computer systems crashed on the start of the second day, 4 more computer systems crashed on the start of the third day and so on, then it took 8 more days to finish the assignment. The value of $\mathrm{m}$ is equal to:

JEE Main 2024 (06 Apr Shift 2)

Options

• A: 150
• B: 180
• C: 160
• D: 125

Question

If each term of a geometric progression ${\mathrm{a}}_1,{\mathrm{a}}_2,{\mathrm{a}}_3,\dots$ with ${\mathrm{a}}_1=\frac{1}{8}$ and ${\mathrm{a}}_2\ne {\mathrm{a}}_1$, is the arithmetic mean of the next two terms and ${\mathrm{S}}_{\mathrm{n}}={\mathrm{a}}_1+{\mathrm{a}}_2+\dots +{\mathrm{a}}_{\mathrm{n}}$, then ${\mathrm{S}}_{20}-{\mathrm{S}}_{18}$ is equal to

JEE Main 2024 (29 Jan Shift 2)

Options

• A: $2^{15}$
• B: $-2^{18}$
• C: $2^{18}$
• D: $-2^{15}$

Question

If three successive terms of a G.P. with common ratio $r\left(r>1\right)$ are the length of the sides of a triangle and $\left[r\right]$ denotes the greatest integer less than or equal to r, then $3\left[r\right]+\left[-r\right]$ is equal to:

JEE Main 2024 (01 Feb Shift 2)

Enter your answer

Question

Let the first three terms $2, p$ and $q$, with $q \neq 2$, of a G.P. be respectively the $7^{\text {th }}, 8^{\text {th }}$ and $13^{\text {th }}$ terms of an A.P. If the $5^{\text {th }}$ term of the G.P. is the $n^{\text {th }}$ term of the A.P., then $n$ is equal to:

JEE Main 2024 (04 Apr Shift 1)

Options

• A: 163
• B: 151
• C: 177
• D: 169

Question

Let $a_1, a_2, a_3, \ldots$ be in an arithmetic progression of positive terms. Let $\mathrm{A}_{\mathrm{k}}=\mathrm{a}_1^2-\mathrm{a}_2^2+\mathrm{a}_3^2-\mathrm{a}_4^2+\ldots+\mathrm{a}_{2 \mathrm{k}-1}^2-\mathrm{a}_{2 \mathrm{k}}^2$. If $\mathrm{A}_3=-153, \mathrm{~A}_5=-435$ and $\mathrm{a}_1^2+\mathrm{a}_2^2+\mathrm{a}_3^2=66$, then $\mathrm{a}_{17}-\mathrm{A}_7$ is equal to______

JEE Main 2024 (05 Apr Shift 1)

Enter your answer

Question

Let the positive integers be written in the form :
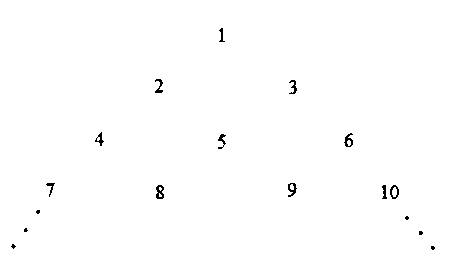
If the $k^{\text {th }}$ row contains exactly $k$ numbers for every natural number $k$, then the row in which the number 5310 will be, is _______

JEE Main 2024 (08 Apr Shift 1)

Enter your answer