Top Previous Year Questions - Gravitation
Question
The mass density of a spherical galaxy varies as over a large distance from its center. In that region, a small star is in a circular orbit of radius . Then the period of revolution, depends on as:
JEE Main 2020 (02 Sep Shift 1)
Options
- A:
- B:
- C:
- D:
Explaination
Question
On the -axis and at a distance from the origin, the gravitational field due to a mass distribution is given by in the -direction. The magnitude of the gravitational potential on the -axis at a distance , taking its value to be zero at infinity is:
JEE Main 2020 (04 Sep Shift 1)
Options
- A:
- B:
- C:
- D:
Explaination
Question
The acceleration due to gravity on the earth's surface at the poles is and angular velocity of the earth about the axis passing through the pole is . An object is weighed at the equator and at a height above the poles by using a spring balance. If the weights are found to be same, then is: (, where is the radius of the earth)
JEE Main 2020 (05 Sep Shift 2)
Options
- A:
- B:
- C:
- D:
Explaination
Question
Two planets have masses and and their radii are a and , respectively. The separation between the centres of the planets is . A body of mass is fired from the surface of the larger planet towards the smaller planet along the line joining their centres. For the body to be able to reach at the surface of smaller planet, the minimum firing speed needed is :
JEE Main 2020 (06 Sep Shift 2)
Options
- A:
- B:
- C:
- D:
Explaination
Question
A satellite of mass is launched vertically upwards with an initial speed from the surface of the earth. After it reaches height ( radius of the earth), it ejects a rocket of mass so that subsequently the satellite moves in a circular orbit. The kinetic energy of the rocket is ( is the gravitational constant; is the mass of the earth):
JEE Main 2020 (07 Jan Shift 1)
Options
- A:
- B:
- C:
- D:
Explaination
Question
Consider two solid spheres of radii , and masses and respectively. The gravitational field due to sphere and are shown. The value of is:
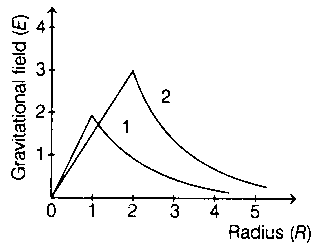
JEE Main 2020 (08 Jan Shift 1)
Options
- A:
- B:
- C:
- D:
Explaination
Question
A body A of mass is moving in a circular orbit of radius about a planet. Another body B of mass collides with A with a velocity which is half the instantaneous velocity of A. The collision is completely inelastic. Then, the combined body:
JEE Main 2020 (09 Jan Shift 1)
Options
- A: continues to move in a circular orbit
- B: Escapes from the Planet's Gravitational field
- C: Falls vertically downwards towards the planet
- D: starts moving in an elliptical orbit around the planet
Explaination
Question
A solid sphere of radius gravitationally attracts a particle placed at from its centre with a force Now a spherical cavity of radius is made in the sphere (as shown in figure) and the force becomes . The value of is:
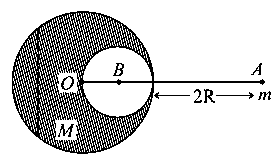
JEE Main 2021 (25 Feb Shift 1)
Options
- A:
- B:
- C:
- D:
Explaination
Question
If one wants to remove all the mass of the earth to infinity in order to break it up completely. The amount of energy that needs to be supplied will be where is ________.
(Round off to the Nearest Integer)
( is the mass of earth, is the radius of earth, is the gravitational constant)
JEE Main 2021 (16 Mar Shift 2)
Enter your answer
Explaination
Question
The variation of acceleration due to gravity with distance from the center of the earth is correctly represented by
(Given radius of earth)
JEE Main 2022 (26 Jun Shift 1)
Options
-
A:
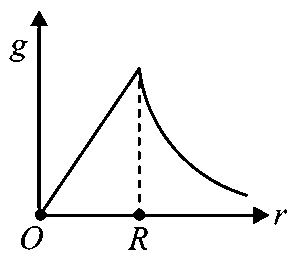
-
B:
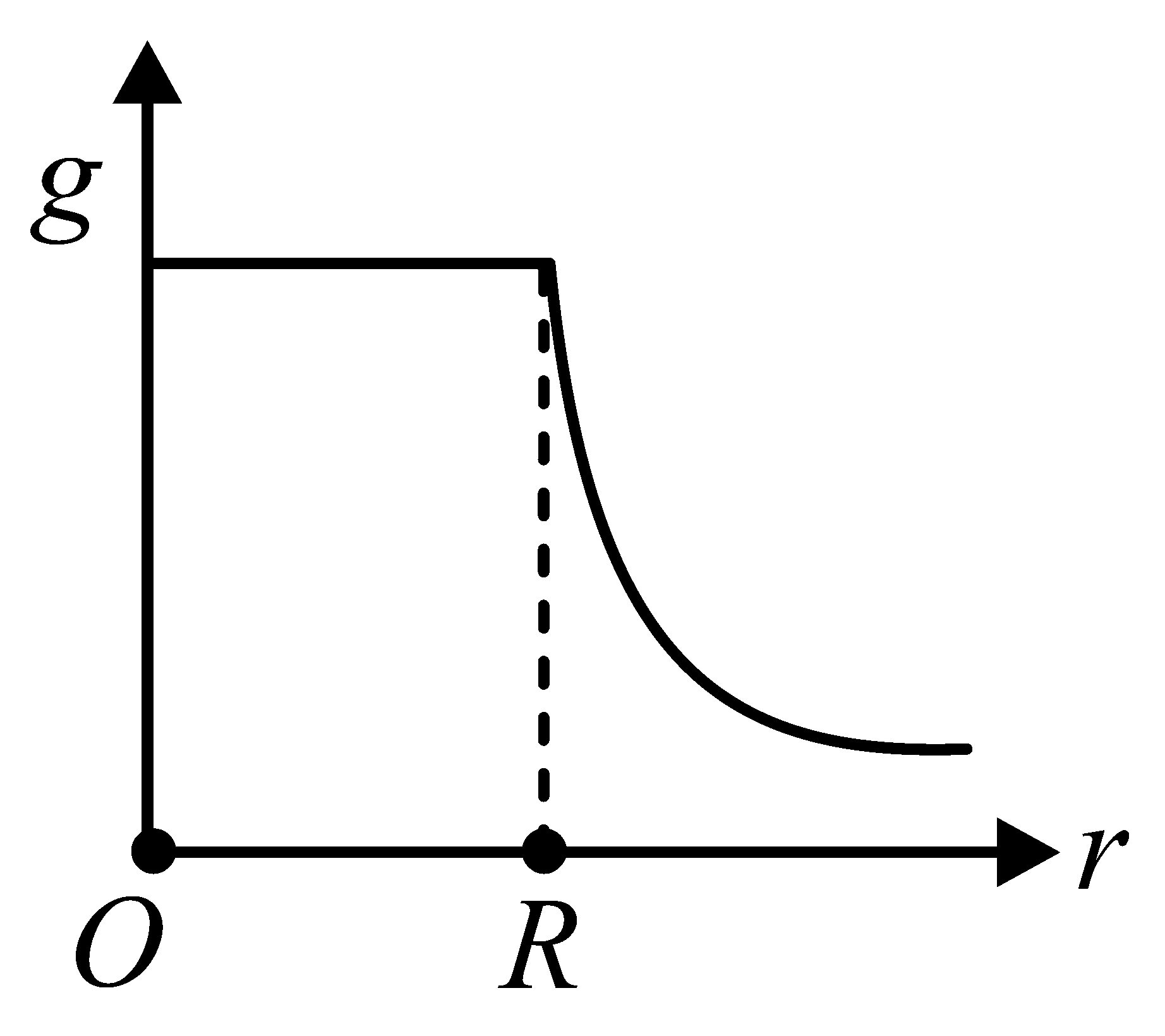
-
C:
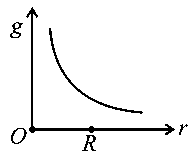
-
D:
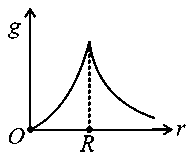
Explaination
Question
An object of mass is taken to a height from the surface of earth which is equal to three times the radius of earth. The gain in potential energy of the object will be
[If, and radius of earth ]
JEE Main 2022 (29 Jul Shift 2)
Options
- A:
- B:
- C:
- D:
Explaination
Question
The escape velocity of a body on a planet is . The escape velocity of the body on another planet , whose density is four times and radius is half of the planet , is
JEE Main 2022 (29 Jun Shift 1)
Options
- A:
- B:
- C:
- D:
Explaination
Question
If earth has a mass nine times and radius twice to the of a planet . Then will be the minimum velocity required by a rocket to pull out of gravitational force of , where ve is escape velocity on earth. The value of is
JEE Main 2023 (01 Feb Shift 1)
Options
- A:
- B:
- C:
- D:
Explaination
Question
If the gravitational field in the space is given as . Taking the reference point to be at with gravitational potential . Find the gravitational potentials at in SI unit (Given, that )
JEE Main 2023 (30 Jan Shift 1)
Options
- A:
- B:
- C:
- D:
Explaination
Question
Correct formula for height of a satellite from earths surface is:
JEE Main 2024 (04 Apr Shift 2)
Options
- A: $\left(\frac{T^2 R^2}{4 \pi^2 g}\right)^{1 / 3}-R$
- B: $\left(\frac{T^2 R^2 g}{4 \pi^2}\right)^{1 / 3}-R$
- C: $\left(\frac{T^2 R^2 g}{4 \pi^2}\right)^{-1 / 3}+R$
- D: $\left(\frac{T^2 R^2 g}{4 \pi}\right)^{1 / 2}-R$
Explaination
Question
In hydrogen like system the ratio of coul0mbian force and gravitational force between an electron and a proton is in the order of :
JEE Main 2024 (05 Apr Shift 1)
Options
- A: $10^{39}$
- B: $10^{29}$
- C: $10^{19}$
- D: $10^{36}$
Explaination
Question
Match List I with List II :

JEE Main 2024 (05 Apr Shift 1)
Options
- A: (A)-(III), (B)-(IV), (C)-(I), (D)-(II)
- B: (A)-(II), (B)-(I), (C)-(IV), (D)-(III)
- C: (A)-(I), (B)-(II), (C)-(III), (D)-(IV)
- D: (A)-(I), (B)-(IV), (C)-(II), (D)-(III)
Explaination
Question
Two planets $A$ and $B$ having masses $m_1$ and $m_2$ move around the sun in circular orbits of $r_1$ and $r_2$ radii respectively. If angular momentum of $A$ is $L$ and that of $B$ is $3 \mathrm{~L}$, the ratio of time period $\left(\frac{T_A}{T_B}\right)$ is:
JEE Main 2024 (08 Apr Shift 1)
Options
- A: $\left(\frac{r_2}{r_1}\right)^{\frac{3}{2}}$
- B: $\frac{1}{27}\left(\frac{m_2}{m_1}\right)^3$
- C: $27\left(\frac{m_1}{m_2}\right)^3$
- D: $\left(\frac{r_1}{r_2}\right)^3$
Explaination
Question
A satellite of $10^3 \mathrm{~kg}$ mass is revolving in circular orbit of radius $2 R$. If $\frac{10^4 R}{6} J$ energy is supplied to the satellite, it would revolve in a new circular orbit of radius (use $g=10 \mathrm{~m} / \mathrm{s}^2, R=$ radius of earth)
JEE Main 2024 (09 Apr Shift 2)
Options
- A: $2.5 R$
- B: $3 R$
- C: $4 R$
- D: $6 R$
Explaination
Question
Four identical particles of mass are kept at the four corners of a square. If the gravitational force exerted on one of the masses by the other masses is , the length of the sides of the square is
JEE Main 2024 (31 Jan Shift 1)
Options
- A:
- B:
- C:
- D:
Explaination
Question
At what distance above and below the surface of the earth a body will have same weight? (Take radius of earth as )
JEE Main 2024 (29 Jan Shift 1)
Options
- A:
- B:
- C:
- D:
Explaination
Question
Given below are two statements : one is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A) : The angular speed of the moon in its orbit about the earth is more than the angular speed of the earth in its orbit about the sun.
Reason (R): The moon takes less time to move around the earth than the time taken by the earth to move around the sun.
In the light of the above statements, choose the most appropriate answer from the options given below :
JEE Main 2024 (27 Jan Shift 2)
Options
- A: (A) is correct but (R) is not correct
- B: Both (A) and (R) are correct and (R) is the correct explanation of A.
- C: Both (A) and (R) are correct but (R) is not the correct explanation of A.
- D: (A) is not correct but (R) is correct