Top Previous Year Questions - Kinetic Theory of Gases
Question
A gas mixture consists of moles of oxygen and moles of argon at temperature . Assuming the gases to be ideal and the oxygen bond to be rigid, the total internal energy (in units of ) of the mixutre is :
JEE Main 2020 (02 Sep Shift 1)
Options
- A:
- B:
- C:
- D:
Explaination
Question
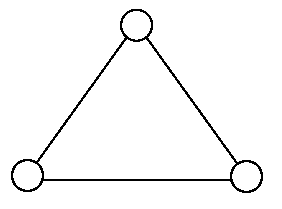
Consider a gas of triatomic molecules. The molecules are assumed to be triangular and made of massless rigid rods whose vertices are occupied by atoms. The internal energy of a mole of the gas at temperature T is:
JEE Main 2020 (03 Sep Shift 1)
Options
- A:
- B:
- C:
- D:
Explaination
Question
In a dilute gas at pressure and temperature '', the time between successive collision of a molecule varies with as :
JEE Main 2020 (06 Sep Shift 2)
Options
- A:
- B:
- C:
- D:
Explaination
Question
The plot that depicts the behavior of the mean free time (time between two successive collisions) for the molecules of an ideal gas, as a function of temperature qualitatively, is: (Graphs are schematic and not drawn to scale)
JEE Main 2020 (08 Jan Shift 1)
Options
-
A:
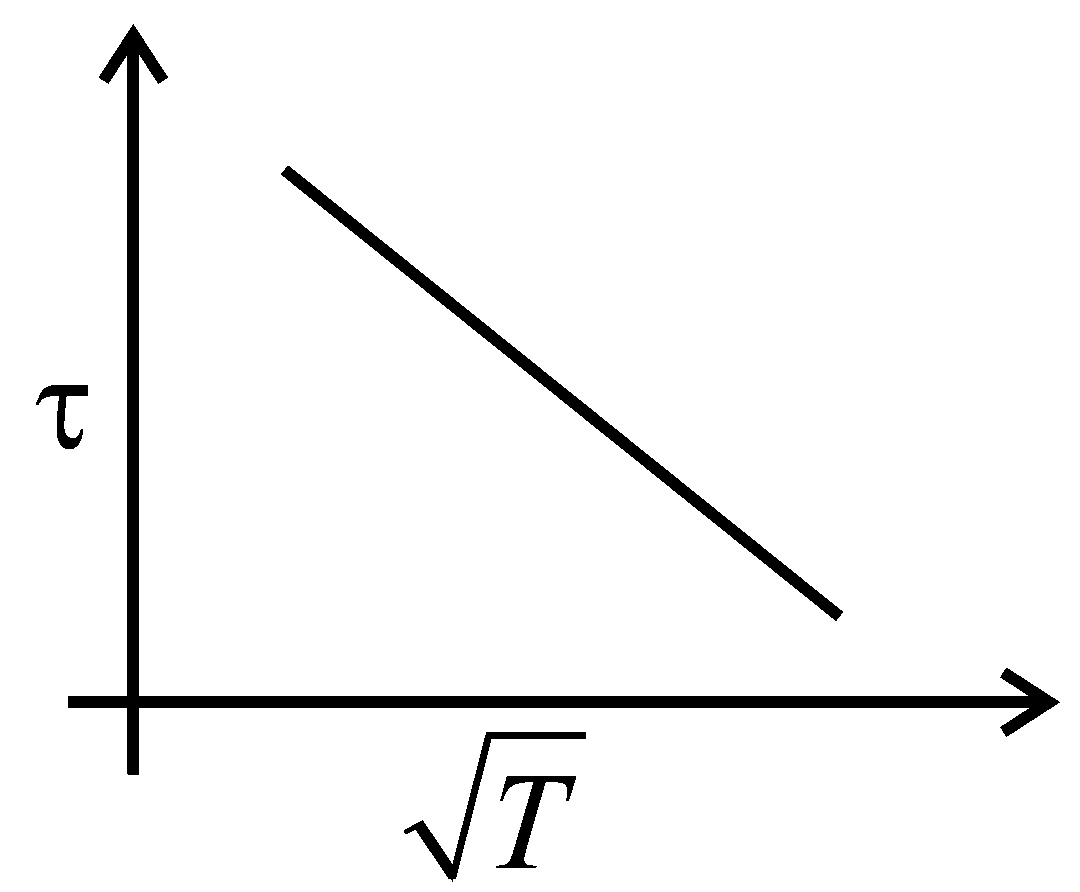
-
B:
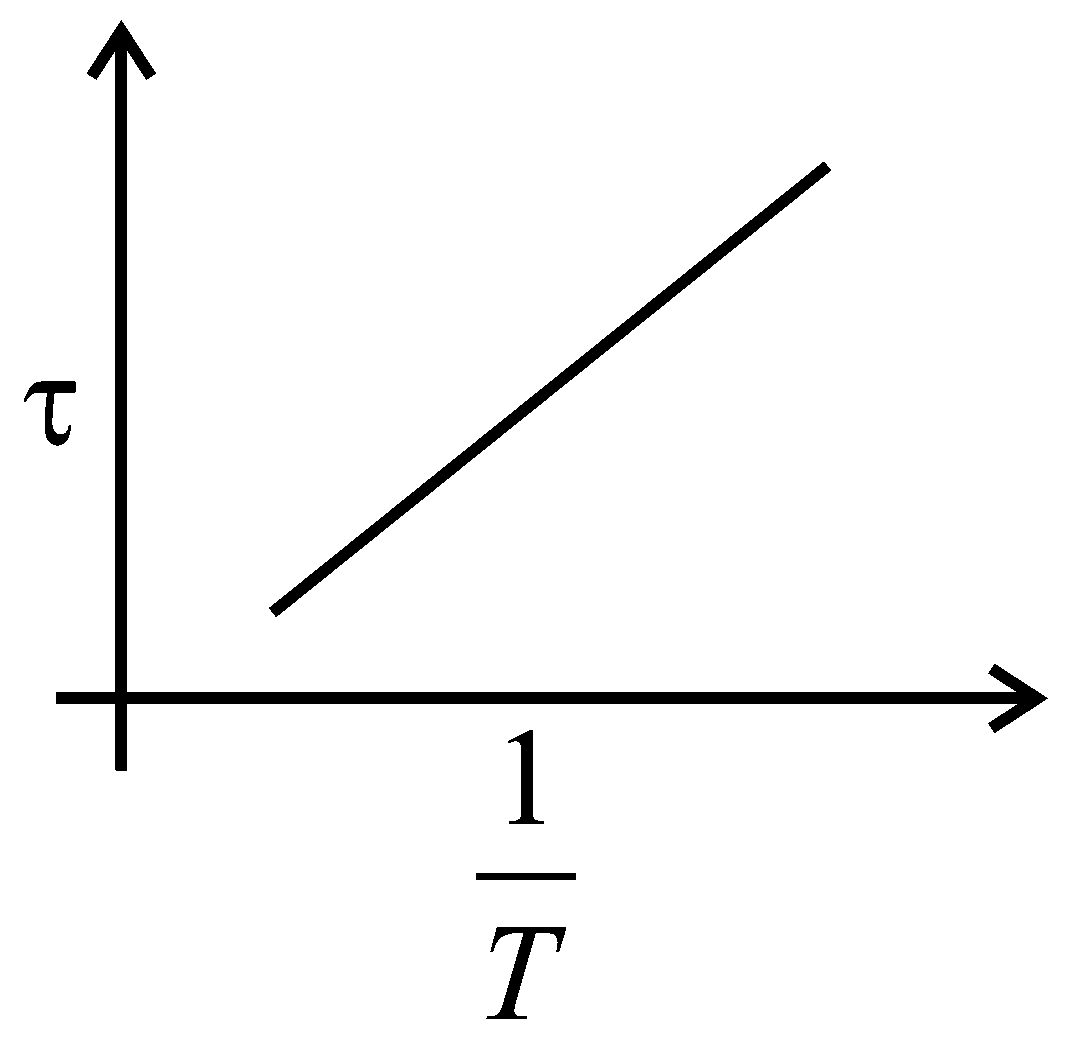
-
C:
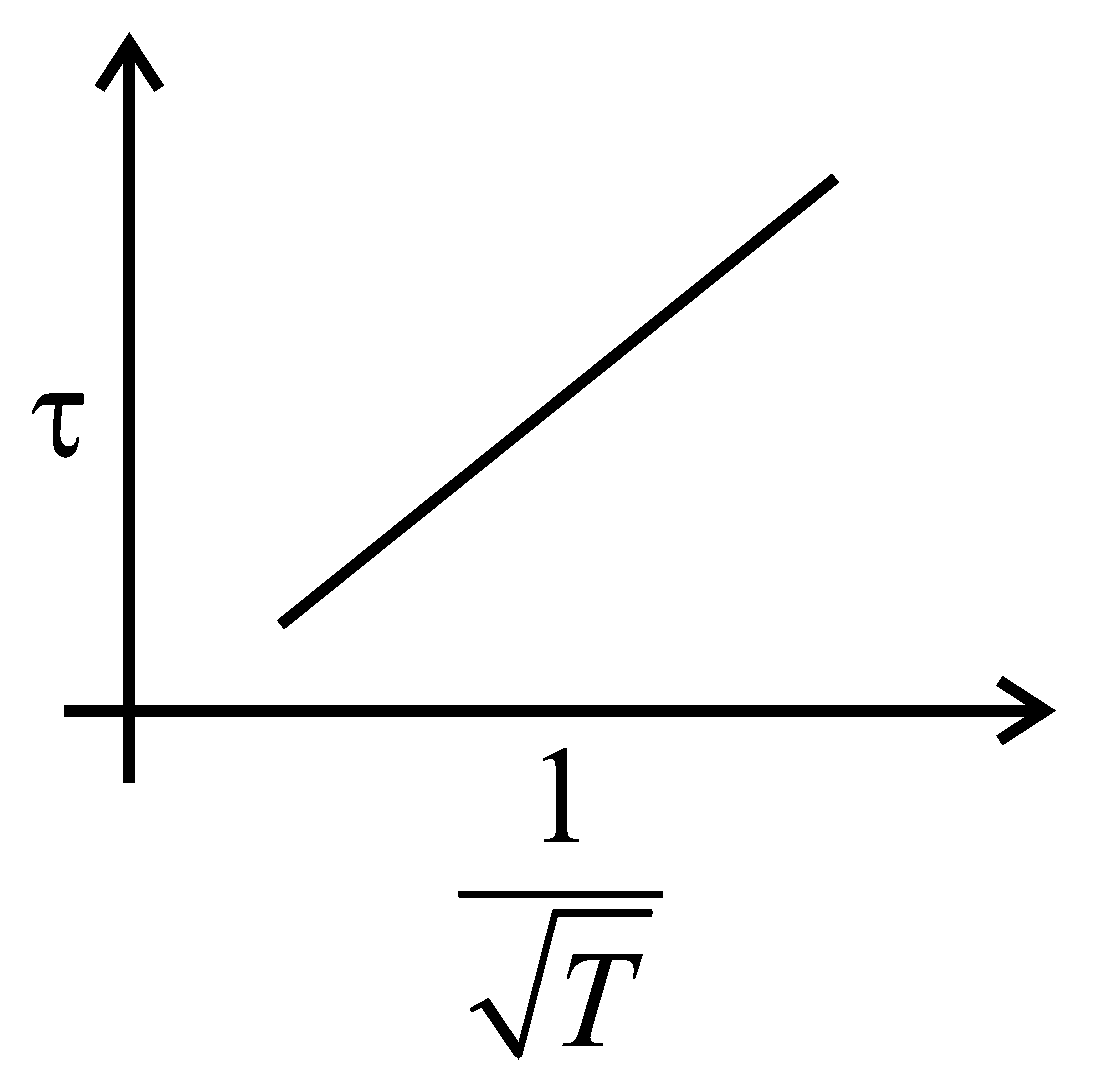
-
D:
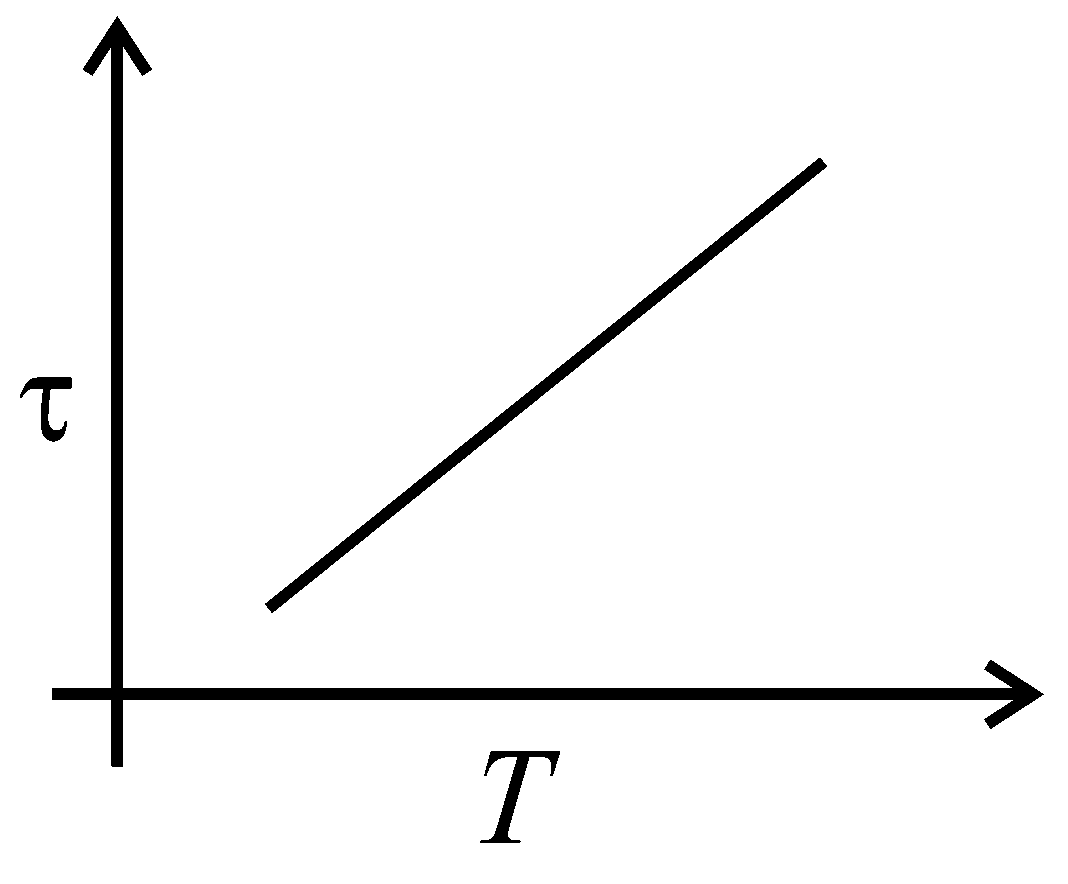
Explaination
Question
Two ideal polyatomic gases at temperatures and are mixed so that there is no loss of energy. If and and and be the degrees of freedom, masses, number of molecules of the first and second gas respectively, the temperature of mixture of these two gases is:
JEE Main 2021 (17 Mar Shift 1)
Options
- A:
- B:
- C:
- D:
Explaination
Question
If one mole of the polyatomic gas is having two vibrational modes and is the ratio of molar specific heats for polyatomic gas then the value of is :
JEE Main 2021 (17 Mar Shift 2)
Options
- A:
- B:
- C:
- D:
Explaination
Question
Consider a mixture of gas molecule of types and having masses The ratio of their root mean square speeds at normal temperature and pressure is:
JEE Main 2021 (20 Jul Shift 1)
Options
- A:
- B:
- C:
- D:
Explaination
Question
A gas has degrees of freedom. The ratio of specific heat of gas at constant volume to the specific heat of gas at constant pressure will be
JEE Main 2022 (26 Jul Shift 2)
Options
- A:
- B:
- C:
- D:
Explaination
Question
Same gas is filled in two vessels of the same volume at the same temperature. If the ratio of the number of molecules is , then
. The r.m.s. velocity of gas molecules in two vessels will be the same.
. The ratio of pressure in these vessels will be .
. The ratio of pressure will be .
. The r.m.s. velocity of gas molecules in two vessels will be in the ratio of .
JEE Main 2022 (27 Jul Shift 1)
Options
-
A:
and only
- B: and only
- C: and only
- D: and only
Explaination
Question
Which statements are correct about degrees of freedom?
A. A molecule with degrees of freedom has different ways of storing energy.
B. Each degree of freedom is associated with average energy per mole.
C. A monoatomic gas molecule has rotational degree of freedom where as diatomic molecule has rotational degrees of freedom
D. has a total to degrees of freedom.
Choose the correct answer from the option given below:
JEE Main 2022 (27 Jul Shift 2)
Options
- A: and only
- B: and only
- C: and only
- D: and only
Explaination
Question
A mixture of hydrogen and oxygen has volume , temperature , pressure and mass . The ratio of number of moles of hydrogen to number of moles of oxygen in the mixture will be
[Take gas constant ]
JEE Main 2022 (27 Jun Shift 1)
Options
- A:
- B:
- C:
- D:
Explaination
Question
The number of air molecules per is increased from to The ratio of collision frequency of air molecules before and after the increase in number respectively is :
JEE Main 2023 (06 Apr Shift 1)
Options
- A:
- B:
- C:
- D:
Explaination
Question
The speed of oxygen molecule in a vessel at particular temperature is when is the average speed of the molecule. The value of will be:
(take )
JEE Main 2023 (13 Apr Shift 1)
Options
- A:
- B:
- C:
- D:
Explaination
Question
The mean free path of molecules of a certain gas at STP is , where is the diameter of the gas molecules. While maintaining the standard pressure, the mean free path of the molecules at is approximately:
JEE Main 2023 (13 Apr Shift 2)
Options
- A:
- B:
- C:
- D:
Explaination
Question
If $\mathrm{n}$ is the number density and $\mathrm{d}$ is the diameter of the molecule, then the average distance covered by a molecule between two successive collisions (i.e. mean free path) is represented by :
JEE Main 2024 (05 Apr Shift 2)
Options
- A: $\sqrt{2} \mathrm{n} \pi \mathrm{d}^2$
- B: $\frac{1}{\sqrt{2 n \pi d^2}}$
- C: $\frac{1}{\sqrt{2} n \pi d^2}$
- D: $\frac{1}{\sqrt{2} n^2 \pi^2 d^2}$
Explaination
Question
The specific heat at constant pressure of a real gas obeying $P V^2=R T$ equation is:
JEE Main 2024 (06 Apr Shift 1)
Options
- A: $\frac{R}{3}+C_V$
- B: $C_V+R$
- C: $C_V+\frac{R}{2 V}$
- D: $R$
Explaination
Question
Given below are two statements : Statement (I) : The mean free path of gas molecules is inversely proportional to square of molecular diameter. Statement (II) : Average kinetic energy of gas molecules is directly proportional to absolute temperature of gas. In the light of the above statements, choose the correct answer from the options given below :
JEE Main 2024 (08 Apr Shift 2)
Options
- A: Statement I is true but Statement II is false
- B: Both Statement I and Statement II are false
- C: Both Statement I and Statement II are true
- D: Statement I is false but Statement II is true
Explaination
Question
The temperature of a gas having molecules per cubic meter at (Given, is :
JEE Main 2024 (29 Jan Shift 2)
Options
- A:
- B:
- C:
- D:
Explaination
Question
Two thermodynamical process are shown in the figure. The molar heat capacity for process and are and . The molar heat capacity at constant pressure and constant volume are represented by and , respectively. Choose the correct statement.
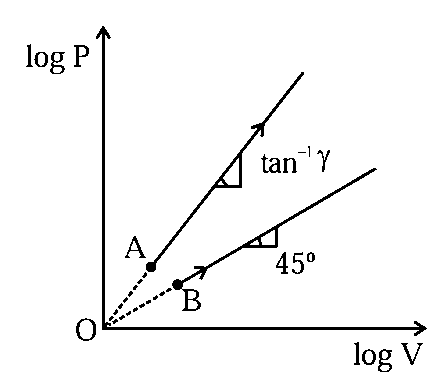
JEE Main 2024 (30 Jan Shift 1)
Options
- A:
- B: and
- C:
- D: