Top Previous Year Questions - Oscillations
Question
A ring is hung on a nail. It can oscillate, without slipping or sliding (i) in its plane with a time period and (ii) back and forth in a direction perpendicular to its plane, with a period . The ratio will be :
JEE Main 2020 (05 Sep Shift 2)
Options
- A:
- B:
- C:
- D:
Explaination
Question
An object of mass is suspended at the end of a massless wire of length and area of cross-section, A. Young modulus of the material of the wire is . If the mass is pulled down slightly its frequency of oscillation along the vertical direction is :
JEE Main 2020 (06 Sep Shift 1)
Options
- A:
- B:
- C:
- D:
Explaination
Question
A mass of is connected to a spring. The potential energy curve of the simple harmonic motion executed by the system is shown in the figure. A simple pendulum of length has the same period of oscillation as the spring system. What is the value of acceleration due to gravity on the planet where these experiments are performed ?
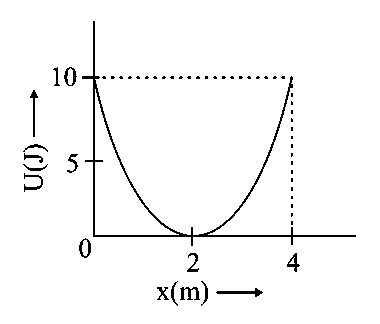
JEE Main 2021 (01 Sep Shift 2)
Options
- A:
- B:
- C:
- D:
Explaination
Question
A particle is making simple harmonic motion along the -axis. If at a distances and from the mean position the velocities of the particle are and , respectively. The time period of its oscillation is given as:
JEE Main 2021 (20 Jul Shift 2)
Options
- A:
- B:
- C:
- D:
Explaination
Question
In the given figure, a body of mass is held between two massless springs, on a smooth inclined plane. The free ends of the springs are attached to firm supports. If each spring has spring constant the frequency of oscillation of given body is:
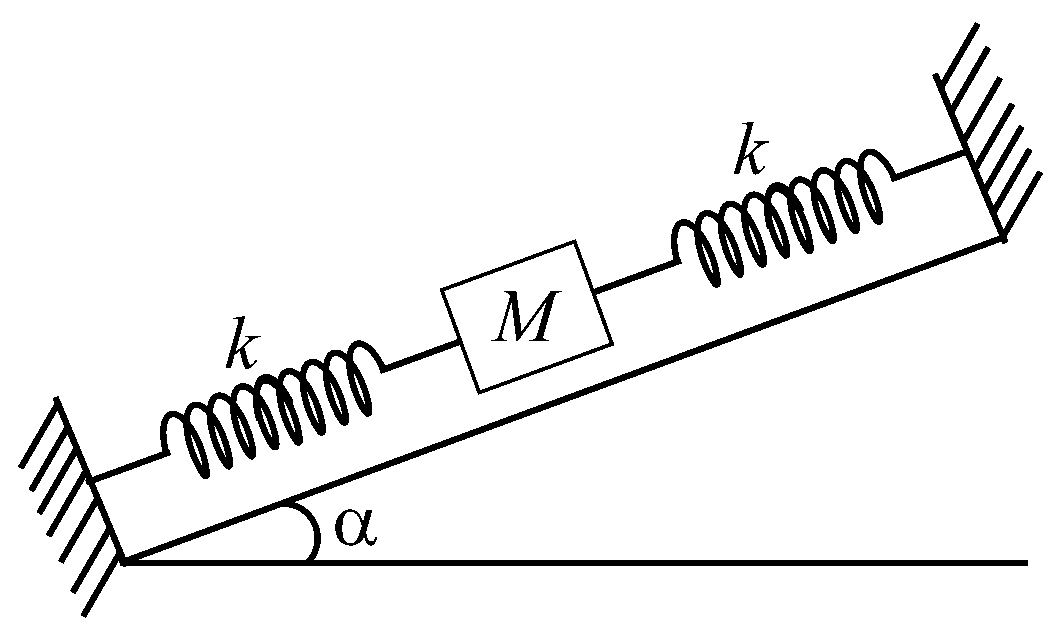
JEE Main 2021 (24 Feb Shift 2)
Options
- A:
- B:
- C:
- D:
Explaination
Question
The point moves with a uniform speed along the circumference of a circle of radius and covers in . The perpendicular projection from on the diameter represents the simple harmonic motion of . The restoration force per unit mass when touches will be :
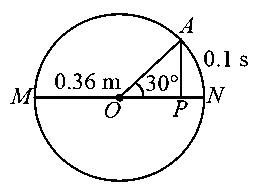
JEE Main 2021 (25 Feb Shift 2)
Options
- A:
- B:
- C:
- D:
Explaination
Question
The variation of displacement with time of a particle executing free simple harmonic motion is shown in the figure.
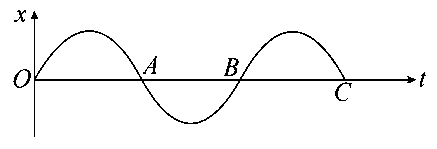
The potential energy versus time plot of the particle is correctly shown in figure:
JEE Main 2021 (27 Aug Shift 1)
Options
-
A:
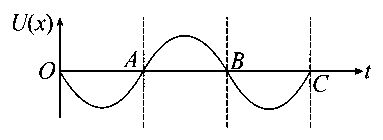
-
B:
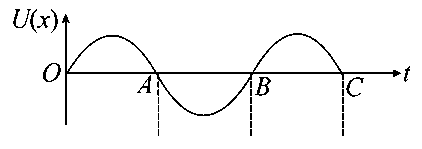
-
C:
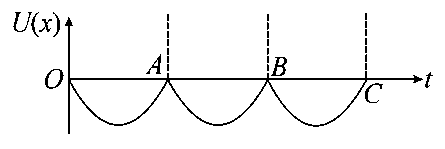
-
D:
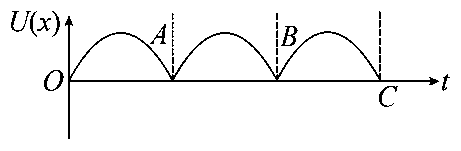
Explaination
Question
Consider two identical springs each of spring constant and negligible mass compared to the mass as shown. Fig. shows one of them and Fig. shows their series combination. The ratios of time period of oscillation of the two SHM is where value of is ______.
(Round off to the Nearest Integer)
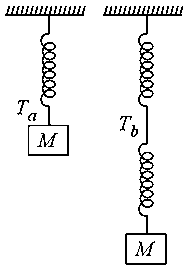
JEE Main 2021 (17 Mar Shift 1)
Enter your answer
Explaination
Question
Two simple harmonic motion, are represented by the equations
Ratio of amplitude of to . The value of is
JEE Main 2021 (27 Aug Shift 2)
Enter your answer
Explaination
Question
The potential energy of a particle of mass in motion along the -axis is given by . The time period of the particle for small oscillation . The value of is _____ .
JEE Main 2022 (28 Jul Shift 2)
Enter your answer
Explaination
Question
A particle executes simple harmonic motion between . If time taken by particle to go from to is ; then time taken by particle in going from to is:
JEE Main 2023 (25 Jan Shift 2)
Options
- A:
- B:
- C:
- D:
Explaination
Question
For particle revolving round the centre with radius of circular path and regular velocity , as shown in below figure, the projection of on the -axis at time is

JEE Main 2023 (08 Apr Shift 2)
Options
- A:
- B:
- C:
- D:
Explaination
Question
In the figure given below. a block of mass placed on a frictionless table is connected with two springs having same spring constant (). If the block is horizontally displaced through then the number of complete oscillations it will make in seconds will be ______.
JEE Main 2023 (31 Jan Shift 1)
Enter your answer
Explaination
Question
The position, velocity and acceleration of a particle executing simple harmonic motion are found to have magnitudes of $4 \mathrm{~m}, 2 \mathrm{~ms}^{-1}$ and $16 \mathrm{~ms}^{-2}$ at a certain instant. The amplitude of the motion is $\sqrt{x}, \mathrm{~m}$ where $x$ is ________
JEE Main 2024 (09 Apr Shift 1)
Enter your answer
Explaination
Question
A particle performs simple harmonic motion with amplitude . Its speed is increased to three times at an instant when its displacement is . The new amplitude of motion is . The value of is _____.
JEE Main 2024 (31 Jan Shift 1)
Enter your answer
Explaination
Question
A simple pendulum is placed at a place where its distance from the earth's surface is equal to the radius of the earth. If the length of the string is , then the time period of small oscillations will be _________.
take ]